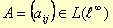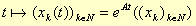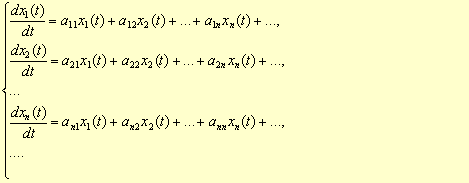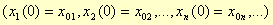Maria GRAMEGNA

(1887-1915)

Nata a Tortona (Alessandria) l'11 maggio 1887 da Maria Cristina Agosta e da Innocenzo Gramegna, Maria Paola Gramegna compie gli studi secondari al R. Liceo "Severino Grattoni" di Voghera, dove all'epoca insegnava l'analista Giuseppe Vitali, e nel novembre del 1906 si iscrive al corso di laurea in Matematica dell'Università di Torino.
Allieva di G. Peano nei corsi di Calcolo infinitesimale e di Analisi superiore, è una studentessa di promettente talento che, grazie al suo curriculum, ottiene una borsa di studio al Collegio delle Province 'Carlo Alberto'. Il 7 luglio 1910 consegue la laurea con il massimo dei voti (110/110), discutendo la tesi Serie di equazioni differenziali lineari ed equazioni integro-differenziali, diretta da Peano. Egli le aveva suggerito di stabilire le risolventi per i sistemi infiniti di equazioni differenziali lineari e per alcuni tipi di equazioni integro-differenziali, temi d'avanguardia nella prima decade del 1900, dibattuti a livello nazionale e internazionale da S. Pincherle, V. Volterra, I. Fredholm, D. Hilbert, F. Riesz, M. Fréchet e E. H. Moore. La ricerca condotta nella tesi, andata purtroppo perduta, è di grande rilievo per l'originalità dei problemi affrontati e delle tecniche adoperate, tanto che, quattro mesi prima dell'esame di laurea, Peano la presenta all'Accademia delle Scienze di Torino, nella seduta del 13 marzo 1910. Nella nota Serie di equazioni differenziali lineari ed equazioni integro-differenziali Gramegna applica il metodo delle approssimazioni successive fornendo l'estensione al caso infinito del risultato ottenuto da Peano, per sistemi di n equazioni, nell'articolo Integrazione per serie delle equazioni differenziali lineari [Atti della R. Accademia delle Scienze di Torino, 22, 1887, pp. 437-446; Mathematische Annalen, 32, 1888, pp. 450-456]. L'obiettivo di Gramegna è di dimostrare il teorema: sia

allora la serie esponenziale e^At converge, e la funzione

è l'unica soluzione del sistema

con le assegnate condizioni iniziali

L'utilizzo di concetti e di metodi innovativi - fra cui quelli della teoria delle matrici infinite e degli operatori lineari definiti su spazi funzionali - e l'approccio astratto e rigorosamente formalizzato, conferiscono un taglio di spiccata modernità alla ricerca di Gramegna. Il suo lavoro, contraddistinto dal ricorso al linguaggio logico-simbolico e al Formulario Mathematico (1908), fornisce spunti interessanti per valutare l'origine e le prime linee di sviluppo delle ricerche di analisi funzionale condotte nella scuola di Peano e consente di evidenziare le difficoltà incontrate dai contemporanei nella loro ricezione e i mutui legami con gli studi di algebra lineare svolti da Peano e da Pincherle fra il 1887 e il 1901 e con le ricerche di analisi generale ad opera di Fréchet e di Moore negli anni 1910-1928.
Conseguito il Diploma di Magistero il 19 luglio 1910, Gramegna intraprende la carriera di insegnante nella scuola secondaria e, vinto il concorso per le Scuole Normali, nel 1911 prende servizio presso la R. Scuola Normale di Avezzano, dove assumerà anche la direzione del Collegio municipale. Nel 1913, pur avendo l'opportunità di trasferirsi a Piacenza, sceglie di restare ad Avezzano, dove muore tragicamente il 13 gennaio 1915, vittima del terremoto.

PUBBLICAZIONI
Gramegna M., Serie di equazioni differenziali lineari ed equazioni integro-differenziali, Atti della R. Accademia delle Scienze di Torino, 45, 1910, pp. 469-491.

NECROLOGI
Mago V., In memoria di Maria Gramegna, Bollettino di Matematica (A. Conti), 13, 1915, p. 304.

FONTI ARCHIVISTICHE
Accademia delle Scienze di Torino, Verbali originali, Classe di Scienze Fisiche e Matematiche, ms. Mazzo 27, 1895-1920, p. 291.
Archivio Storico dell'Università di Torino, Facoltà di Scienze MFN, ms. VII, 83, Verbali delle adunanze della Facoltà di Scienze MFN; ms. VII, 86, Programmi dei corsi liberi 1909-10/1916-17; ms. XI, F 7, 1904-1912, Studenti. Domande numerate, con ordinamento alfabetico e cronologico. Fascicoli dei concorrenti ai posti nel Collegio Carlo Alberto; ms. XI, F 22, Concorso 1906; ms. XI, F 31, Rubrica degli studenti, informazioni, 1906-1913; ms. X, D, 58, Verbali degli Esami Speciali di Calcolo infinitesimale 18.6.1902-22.3.1921, p. 202; ms. X, D, 63, Verbali degli Esami Speciali di Analisi superiore 16.6.1902-28.10.1955, p. 14.
Segreteria studenti della Facoltà di Scienze MFN, Università di Torino: Registro di Carriera Scolastica della Facoltà di Scienze, n° 31, p. 58; Verbali di Laurea della Facoltà di Scienze dal 4.7.1902-14.4.1921, Maria Gramegna, n° matr. 1258.
Archivio di Stato, Sezione di Avezzano, Liceo 'A. Torlonia' e R. Scuola Normale Femminile 'Maria Clotilde di Savoja', Stato Personale di Maria Gramegna 1913-1915, ff. 9-11.

FONTI BIBLIOGRAFICHE
Giacardi L., Gramegna Maria, Dizionario Biografico degli Italiani, Roma, vol. 58, Istituto dell'Enciclopedia Italiana Treccani, 2002, pp. 398-399.
Luciano E., At the origins of functional analysis: G. Peano and M. Gramegna on Ordinary differential equations, Revue d'Histoire des Mathématiques, 12, 2006, pp. 33-77.
Tricomi F., Matematici Italiani del primo secolo dello stato unitario, Memorie dell'Accademia delle Scienze di Torino, Classe di Scienze FMN, 4, 1962, p. 61.

Erika Luciano