Quaderno di 76 carte, 157×105 mm. Contiene: Indice; Parte 1ª: Introduzione. Generalità (1 r.); Coordinate projettive (2r.); Forme di 1a specie (2r.-3r.); Forme di 2a specie (3r.-5r.); Spazio (5r.-9r.); Generalità sulle varietà algebriche (9r.-28r.); Parte 2ª: Sulle questioni numerative (29 r.); Dimensione di una varietà(29r.-30r.); Dimensione di una condizione (30r.-32r. ); Sui problemi determinati (32r.-34r.); Principio della conservazione del numero (35r.-39r.); Principio di corrispondenza (39r.-46r.); Cenni sulle caratteristiche (46r.-55r.); Parte 3ª: Sulle curve piane e superficie (specialm. rigate) algebriche (56 r.); Curve piane (56r.-66r.); Superficie (66r.-71r.).
Quaderno
di 108 pagine, 146×100 mm, numerate in due serie: le pagine da 1
a 54 si riferiscono all'argomento indicato nel titolo e contengono: Parte
1ª : Introduzione. Generalità (1-41); Parte 2ª
: Curve e superficie e loro caratteri (41-54). La seconda serie,
numerata da 1 a 16, si riferisce agli argomenti trattati nell'anno 1895-96
e precisamente:
Preliminari (1-2); Elementi imaginari (2-3);
Antiprojettiv.à
(3-7); Introduzione alla geometria degl'iperspazi (7-9); Varietà
generate da forme projettive (9-13); Cenno sulle var.à
f(x)=0 d'ord. n (13-15); Cenni sulla geometria della retta (15-16).
Introduzione
a cura di Alberto Conte. Quaderno di 218 pagine più 1 carta
incollata alla pagina 1 riportante l'Indice, 158×108 mm. Contiene:
Cap.1°.
Preliminari (1-12); Cap.2°. Degl'iperspazi (13-46); Cap.3°.
Oggetto della Geometria su una ¥1
algebrica. Corrispondenze algebr e. Serie lineari (47-67);
Cap.
4°. Geometria sugli enti razionali (68-81); Cap. 5°. Serie
lineari ¥1.
Genere degli enti algebrici (82-103); Cap.
6°. Formula di Zeuthen. Varietà ¥1
di spazi e loro applicazioni. Le serie speciali (104-129); Cap.
7°. Serie complete. Serie residue. Curve aggiunte. Applicazioni
(129-143); Cap. 8°. Il metodo algebrico di Brill e Nöther
(144-156); Cap. 9°. Rappres.i reali dell'ente algebr
o.
Il metodo funzionale di Riemann (157-193); Cap. 10°. I moduli.
Le serie lineari sugli enti generali (194-208); Indice (209).
Quaderno
di 144 pagine, 158×108 mm, cui si aggiungono 34 pagine, 131×91
mm, incollate all'ultima carta del quaderno, la cui numerazione segue quella
principale. Contiene: Introduzione (1-4); Sistemi infiniti di
linee e di superficie (5-17);Sulla geometria della
retta (18-42); Alcune considerazioni geometriche sulle equazioni
differenziali di 1° ordine (43-91); Sulle linee nello spazio
(92-112); Delle superficie. Preliminari (113-121); Linee coniugate.
Asintotiche (122-127); Curvatura delle superficie (128-139);
Geodetiche (140-151); Rappresentaz.i conformi
(152-154); Superficie applicabili. Geometria della superficie (155-173).
Quaderno
di 184 pagine, 158×105 mm, più 2 carte incollate rispettivamente
alle pagine 5 e 128. Il quaderno riunisce le lezioni svolte durante gli
anni 1892-93 e 1893-94. Le pagine numerate da 1 a 68 si riferiscono all'anno
1892-93 e contengono: Cap. 1°. Preliminari. Iperspazi (1-34);
Oggetto della Geometria su una varietà algebrica. Corrispondenze.
Serie lineari (34-45); Le serie lineari sulle curve algebriche
(45-68). Le pagine numerate da 71 a 180 si riferiscono all'anno 1893-94
e contengono: Preliminari (71-73); Superficie razionali e loro
rappresentaz.i piane (74-100); Su alcuni caratteri dei
sistemi lineari (101-128); Trasformazioni Cremoniane (128-141);
Trasformaz.i quadratiche (141-180).
Introduzione
a cura di Paola Gario. Quaderno di 174 pagine, 168×113 mm. Contiene:
Preliminari:
Coordinate, Elementi imaginari, Curve e superficie algebriche, Prime nozioni
sui punti singolari, Intersezioni di due curve, Restrizioni al numero dei
punti multipli di una curva (1-16); Teoria della polarità
(16-20); Applicazioni. Curve-inviluppi. Prime singolarità (21-51);
Le formole di Plücker (52-56); Cenni sulle trasformaz.i
birazionali piane (57-60); Risoluzione e studio
delle singolarità mediante trasformaz.i
quadrat.e (61-78); Genere (78-89);
Studio delle singolarità mediante gli sviluppi in serie (90-106);
Calcolo degli sviluppi in serie (106-129); Applicazione degli
sviluppi in serie alla determinazione dei caratteri di una curva (130-168);
Indice.
Quaderno
di 226 pagine, 173×118 mm. Contiene: Indice;
Fisica
Matematica. Introduzione (1-6); Teoria del
potenziale: Forze Newtoniane (7-11), Caso che il punto potenziato
stia nelle masse agenti (11-14), Allontanamento indefinito del punto
potenziato (14-15), Un caso particolare (15-19), L'equazione
di Laplace per punti esterni (19-20), Nuove espressioni per X, Y,
Z (20-24), Trasformazione
dell'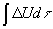 .Equazione di Poisson(24-29),
Caratteristiche della funzione potenziale di spazio (30), Funzione
potenziale di superficie (30-32), Funzione potenziale di linea
(32-34), Funzione potenziale di un doppio strato (34-37), Teorema
di Green e prime applicazioni (38-43), Applicazioni del teorema
della media aritmetica (43-50), Teorema di Dirichlet (50-54),
Problema di Green-Dirichlet (55-75), Del potenziale (75-81),
Applicazioni all'Elettrostatica (81-90): Problema generale dell’Elettrostatica
(90-95), Potenziale elettrostatico di un sistema di conduttori (95-96),
Determinazione della distribuzione dell’elettricità su una sfera
(96-101),
Sulle linee di forza (101-106), Dei condensatori
(106-115); Introduzione allo studio dei moti nei mezzi continui: Cinematica
(116-129),
L’equazione alla superficie (129-130), Le pressioni
e le equazioni meccaniche dei moti considerati (131-138),
Variazione
della pressione: pressioni principali (138-143), La pressione su
una superficie di discontinuità (143-144),
Sostituzione delle
forze Newtoniane con pressioni in un mezzo continuo (144-149),
Il
principio di D'Alembert e Lagrange per i mezzi continui (149-153),
Idrodinamica
(153-157), Equilibrio dei fluidi (157-160), Equazioni idrodinamiche
di Eulero e di Lagrange (160-165), Sui moti vorticosi (165-175),
Dei moti con potenziale di velocità (175-181), Moti con
potenziale di velocità dei fluidi incompressibili (o liquidi)
(181-183), Caso del moto stazionario (183-185), Applicazione
delle variabili complesse ai moti stazionari di fluidi incompressibili
con potenziale di velocità (185-190), Moto stazionario del
fluido elettrico (190-202), Moto con potenziale di velocità
dei gas perfetti nel caso dei piccoli moti, senza forze esterne date
(202-205), Alcuni cenni sull'integrazione delle equazioni differ.li
parz.li della Fisica (206-208), Propagazione del calore
in una sbarra (208-213), Vibrazioni sonore in un tubo (213-219).
.Equazione di Poisson(24-29),
Caratteristiche della funzione potenziale di spazio (30), Funzione
potenziale di superficie (30-32), Funzione potenziale di linea
(32-34), Funzione potenziale di un doppio strato (34-37), Teorema
di Green e prime applicazioni (38-43), Applicazioni del teorema
della media aritmetica (43-50), Teorema di Dirichlet (50-54),
Problema di Green-Dirichlet (55-75), Del potenziale (75-81),
Applicazioni all'Elettrostatica (81-90): Problema generale dell’Elettrostatica
(90-95), Potenziale elettrostatico di un sistema di conduttori (95-96),
Determinazione della distribuzione dell’elettricità su una sfera
(96-101),
Sulle linee di forza (101-106), Dei condensatori
(106-115); Introduzione allo studio dei moti nei mezzi continui: Cinematica
(116-129),
L’equazione alla superficie (129-130), Le pressioni
e le equazioni meccaniche dei moti considerati (131-138),
Variazione
della pressione: pressioni principali (138-143), La pressione su
una superficie di discontinuità (143-144),
Sostituzione delle
forze Newtoniane con pressioni in un mezzo continuo (144-149),
Il
principio di D'Alembert e Lagrange per i mezzi continui (149-153),
Idrodinamica
(153-157), Equilibrio dei fluidi (157-160), Equazioni idrodinamiche
di Eulero e di Lagrange (160-165), Sui moti vorticosi (165-175),
Dei moti con potenziale di velocità (175-181), Moti con
potenziale di velocità dei fluidi incompressibili (o liquidi)
(181-183), Caso del moto stazionario (183-185), Applicazione
delle variabili complesse ai moti stazionari di fluidi incompressibili
con potenziale di velocità (185-190), Moto stazionario del
fluido elettrico (190-202), Moto con potenziale di velocità
dei gas perfetti nel caso dei piccoli moti, senza forze esterne date
(202-205), Alcuni cenni sull'integrazione delle equazioni differ.li
parz.li della Fisica (206-208), Propagazione del calore
in una sbarra (208-213), Vibrazioni sonore in un tubo (213-219).
Introduzione
a cura di Paola Gario. Quaderno di 116 pagine, 176×112 mm, cui si
aggiungono 4 pagine, 170×110 mm, incollate alla copertina al fondo
del quaderno, la cui numerazione segue quella principale. Contiene: Preliminari
(1-2); Prime nozioni sui punti singolari (2-8);
Intersezioni di due curve piane (9-21); Intersezioni di superficie
(21-25); Teoria della polarità (26-38); Applicazioni.
Curve e superficie come inviluppi (38-87); Studio delle singolarità
mediante trasformazioni birazionali e sviluppi in serie (88-117).
Due quaderni
di 202 pagine complessive, 176×112 mm e 172×118 mm.
Il primo
(112 pagine) contiene: Introduzione (1-7); Teoria del potenziale
(8-57); Le formule di Green e loro corollari (57-69); Sulle funzioni
armoniche in dati spazi (69-77); Problema di Green ecc. (77-86);
Metodo della media aritmetica di Carlo Neumann (86-102); Procedimento
alternato di Schwarz, metodi combinatori di C. Neumann (102-108).
Il secondo (90 pagine) contiene: Metodo delle immagini, od inversione (109-112); Trasposizione di masse alla superficie. Strati di livello (113-126); Elettrostatica (127-148 e continua in 159-183); Digressione sulle funzioni sferiche (148-158).