Quaderno
di 252 pagine, 173×116 mm. Contiene: Indice (1); Trattati
(3-4); Introduzione (5-9); Cenni intorno alle superficie
(10-33); Cenni sulla geometria degl'iperspazi (34-42); Geometria
projettiva e geometria elementare della retta (43-48); Le direzioni
nello spazio rigato (49-61); Prime applicazioni alle rigate, congruenze
e complessi (61-88); Proprietà metriche (88-113); Congruenze
normali (113-135); Proprietà d'ordine super.e
delle rigate (135-166); Proprietà d'ordine superiore delle
congruenze (166-180); Proprietà d'ordine superiore dei complessi
(181-193); Le equazioni differenziali nella teoria dei complessi di
rette (194-204). Le pagine 204-237 contengono aggiunte riferite alle
pagine precedenti; quelle scritte alle pagine 204-206 sono datate aprile
1923.
Quaderno
di 244 pagine, 173×118 mm. Contiene: Indice (1); L'astrazione
nella Geom.a moderna (5-11); Sul concetto d'infinito
(12-24); Gli elementi imaginari in Geom.a (24-39); Intorno
alle funzioni con cui si definiscono le varietà geometriche
(39-47); Intorno alle funzioni ecc. (p. 39). Seguito. Passaggio al campo
complesso (47-57); I rami di curve analitiche (57-70); Geometria
generale o differenziale e geometria algebrica (71-74); Generazioni
delle curve e sup. algebr.e (74-92); Sulla Geometria
numerativa (92-118); Trasformazioni e loro gruppi. Vari indirizzi
geometrici (119-122); Esempi. Alcuni indirizzi nella geometria generale
delle
superficie (123-143);
Cenno sulla Geom.a non euclidea
(144-154);
La
Geometria sopra una curva algebrica (155-164);
Uso delle funzioni
ellittiche ecc. nello studio delle curve algebr.e (165-175);
Geometria
delle trasformaz.i biraz.li delle superficie
(176-181).
Le pagine 236-239 contengono aggiunte riferite alle pagine precedenti.
Quaderno
di 232 pagine, 174×116 mm. Contiene: Indice (3); Oggetto
del corso (5-7); Trasformaz.i quadratiche piane (7-11);
Cenni
sulle trasformaz.i Cremoniane in generale (11-20);
Sui
sistemi lineari di forme (21-28); Digressione sugl'iperspazi
(28-30); Ritorno ai sistemi lin.i di forme (31-36); Trasformaz.i
razionali (37-45); Scomposiz.e dei punti multipli delle
curve piane algebriche (46-60); Sulla risoluzione dei punti multipli
delle curve sghembe algebr.e (61-63); Scomposiz.e
dei punti multipli delle superf. algebriche (64-74); Sulla risoluz.
delle singolarità con trasf.i biraz.li delle
curve o superficie (75-79); Generalità sulle serie lineari
(80-92); Le serie lineari ¥1
ed il genere delle curve (92-102); Un carattere delle superficie
(102-117); Serie lineari complete, ecc. (118-125); Il teorema 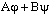 per
curve piane e per superf.e (125-136); Il "Restsatz"
(137-141); Le serie lineari, studiate sulla curva piana (142-147);
Cenni
intorno ai sistemi lineari nel piano o sulle sup. raz.li
(148-155); Cenni intorno alle sup. rigate e alla classe che esse rappresentano
(156-161);
Sulle prime ricerche di caratteri delle superf. invar.i
per trasf. biraz.li(162-167); Seguito. Genere aritmetico
(167-180); Addizione di sistemi lineari. Aggiunzione (180-187);
Sistemi
canonico e pluricanonico. Plurigeneri (187-193); Sul genere lineare
(194-198); Dimensione di un sist. lin.e su una sup. Cenno
sui sist.i non lineari (198-206). Le pagine 218-235 contengono
aggiunte riferite alle pagine precedenti.
per
curve piane e per superf.e (125-136); Il "Restsatz"
(137-141); Le serie lineari, studiate sulla curva piana (142-147);
Cenni
intorno ai sistemi lineari nel piano o sulle sup. raz.li
(148-155); Cenni intorno alle sup. rigate e alla classe che esse rappresentano
(156-161);
Sulle prime ricerche di caratteri delle superf. invar.i
per trasf. biraz.li(162-167); Seguito. Genere aritmetico
(167-180); Addizione di sistemi lineari. Aggiunzione (180-187);
Sistemi
canonico e pluricanonico. Plurigeneri (187-193); Sul genere lineare
(194-198); Dimensione di un sist. lin.e su una sup. Cenno
sui sist.i non lineari (198-206). Le pagine 218-235 contengono
aggiunte riferite alle pagine precedenti.
Introduzione
a cura di Simonetta Di Sieno. Quaderno di 234 pagine, 173×117 mm,
cui si aggiungono altre 12 pagine inserite dopo la pagina 214. Contiene:
Indice
(1);
Introduzione (3-19); Sui campi a più dimensioni
(20-30); Geometria degli elementi differenziali (31-45); Equazioni
differenziali fondam.li per un gruppo continuo finito (45-53); Gruppi
monomi e trasformaz.i infinitesime (53-70);
Gruppi
monomi di projettività sulla retta (70-81); Gruppi monomi
di movimenti nel piano (81-85); Gruppi monomi di collineaz.i
(86-108); Trasformaz.i infinitesime e gruppi monomi contenuti
in un Gr qual.e(109-122); Transitività.
Funzioni e varietà invarianti (122-138); L'alternante di
due trasformaz.i infinitesime. Il teorema principale (139-152);
Determinaz.e
dei gruppi continui finiti nei campi ad 1 dimens. (152-161);
Sulla
determinaz.e dei gruppi continui finiti nel piano (161-183);
Sulla
determinaz.e dei gruppi continui di collineazioni piane
(184-193);
Composizione
dei gruppi (193-202);
Esempio: il G4 lin.e
omog.o piano (203-206);
Un'applicazione dei gruppi alle
equ.i diff.li (207-214);
Ritorno alla composiz.
dei gri: Gruppo aggiunto (214-215d);
Strutture
dei gruppi trinomi (215d-217c).
Le pagine 218a e 219-233 contengono aggiunte riferite alle pagine
precedenti.
Quaderno di 228 pagine,
176×122 mm. Contiene: Indice (1); Introduzione (3-11);
Fasci
di coniche (12-22); Fasci di quadriche. Classific.e
(23-42); Complesso tetraedrale, e sua relaz.e coi fasci di
quadriche (42-51);
La quartica sghemba di 1a
specie (51-68); Generalità sui sistemi lin.i
(68-74); Relaz. armonica fra coniche o quadr.e (74-85);
Sistemi
lin.i ¥3
di coniche. Superf.e imagini (86-93); Seguito. Superf.
di Steiner. Rigate cubiche (93-108); Reti di coniche (109-119);
Trasformazioni
piane legate alle reti di coniche (120-131); Reti di quadriche
(132-139); Le quartiche piane, in relaz. colle reti di C2
e di F2(140-148); Sui sistemi lin. ¥3
di F2 (148-156); La F4 di Kummer e le congruenze
quadratiche di rette (157-169). Le pagine 211-230 contengono aggiunte
riferite alle pagine precedenti.
Quaderno di 168 pagine,
175×120 mm. Contiene: Indice (1); Il concetto d'iperspazio
(3-16); Spazi subordinati (17-25); Cenni sulle projettività
in un Sn (26-31); Prime nozioni sulle curve e varietà
super.i (31-41);
Ancora sulle var.à
algebr.e, in partic.e ipersuperf.e
(41-47); Sulle quadriche iperspaz.li e fasci di quadriche
(48-59);
Geometria
delle rette e geometria delle sfere (59-79);
Varietà generate
da forme fondam.li projettive (79-90);
Sistemi nulli
e complessi lineari di rette (91-118). Le pagine 209-233 contengono
aggiunte riferite alle pagine precedenti.
Quaderno
di 224 pagine, 175×122 mm. Contiene: Indice (3); Oggetto
del corso (5-9); Definizioni e primi esempi d'invarianti (10-16);
Forme
polari, Jacobiani, ecc. (17-23); Alcuni teoremi generali (23-29);
Alcuni
procedimenti per ottenere forme invariantive, specialm.e per
forme binarie (30-46); La notazione simbolica per le forme binarie
(47-58); Polarità. Scorrimenti. Apolarità (59-71);
La
cubica binaria (72-84); La quartica binaria (85-98); Applicazioni
della teoria delle forme binarie alle curve razionali (99-114);
Seguito.
La quartica sghemba razionale (115-126); La notazione simbolica
per le forme ternarie, quaternarie ecc. (127-133);
Principio di
trasporto di Clebsch (134-140); Le pagine 183-233 contengono aggiunte
riferite alle pagine precedenti.
Introduzione
a cura di Franco Fava. Quaderno di 236 pagine, 175×120 mm. Contiene:
Indice
(3);
Alcune citazioni (5-6); Introduzione (7-17); Rette
e piani tangenti (18-29); Cenni
sugl'inviluppi (30-36); Cenni sulle equ.i
differenziali (37-45); Sistemi coniugati di linee su una superficie
(46-60); Asintotiche di alcune classi di superficie (60-74); Sulle
congruenze rettilinee (75-99); Proprietà metriche delle curve
nello spazio (100-127); Proprietà metriche delle superf.e.
L'elemento lineare. Sup.e applicabili (128-142); Curvatura
delle sup. Formole di Gauss, Codazzi. Linee di curvatura (142-171);
Rappresentaz.i
conformi od isogonali (172-177). Le pagine 186-235 contengono aggiunte
riferite alle pagine precedenti.
Quaderno
di 270 pagine, 177×120 mm. Contiene: Indice (5); Cenni
su i fondamenti delle Matematiche, in partic.edella Geom.a(7-27);
Geometria
elem.e e geom.a projettiva (28-49); Geom.
elementare e geom.a delle trasform.i circolari (50-71);
Cenni
sull'Analysis situs (72-83); Sulle costruzioni geometriche (84-100);
Costruzioni
con meccanismi articolati (101-114); I problemi risolubili colla
sola riga (115-126); I problemi risolubili colla riga e col compasso,
o strum.i equiv.i(126-143);
Sulle equazioni
algebriche risolubili per radicali quadratici (144-152);
Applicazioni
ai problemi classici di 3° grado (152-156); Le curve, le cui
intersezioni con rette generiche si ottengono con riga e compasso (157-168);
Il
problema della divisione della circonferenza (168-181); Il problema
della quadratura del cerchio (181-200.5); Principî di Geom.a
non-euclidea (200.5-207). Le pagine 210-231 contengono aggiunte riferite
alle pagine precedenti.